Symmetry

Any individual who has taken a high school or college physics course has likely encountered the idea of symmetry in a physics setting before. A typical example would be in the context of mass or charge distributions, where calculations relating to the gravitational or electric fields of uniformly massive or charged surfaces can be greatly simplified by appealing to symmetry.


An example of employing symmetry to simplify calculations using Gauss’s Law, as any fields generated by the sphere are uniform along the surface $GS$.

However, tricks like these tend to be ad-hoc aids for performing calculations, and are tied to parameters (like the charge distribution) that may vary from system to system; this begs the question — are there symmetries tied more closely to the physical interactions that are, in some way, less sensitive to specific configurations?

This question has significant consequences being explored today in the context of Quantum Field Theory and high energy particle physics. However, it’s easier to start in the world of classical physics and move our way into the modern era to understand how the picture changes as we embrace the added “machinery” that each new theory gives us.

Our story begins with a German mathematician named Emmy Noether in 1915 who proved a significant theorem¹ decribing classical physics, one form of which says

Every differentiable symmetry of a physical system’s Lagrangian implies the conservation of some quantity with respect to time.

This theorem leads to many results that are typically covered in advanced undergraduate physics courses. Using the theorem, it can be shown that invariance of a system’s Lagrangian under small changes in time, linear position, angular position, and electric (scalar and vector) potential leads to the conservation of energy, momentum, angular momentum, and charge, respectively. But what if have symmetries that are not “smooth” in the same sense as translations and rotations in space, and are instead confined to some discrete set of values? We then lose Noether’s Theorem, and it seems we’re back to a situation where the symmetry approach may work for some transformations, but fail for others.

Inversions

Fortunately, three discrete transformations that challenge our recent understanding of physics — charge conjugation, time reversal, and parity inversion — fall under a category of transformations known as inversions (i.e. they are self-inverses). If these transformations are symmetries, we can label each part of a system with $-1$ or $1$ (even or odd), and the product of these labels is in fact conserved. Since these labels can typically be associated with physical observables, we can experimentally verify whether these symmetries are violated by looking for lack of conservation, just like with Noether’s theorem!

Parity

Let’s start by concretely thinking about the parity inversion transformation. Mathematically, this corresponds to negating the components of all position vectors, or, equivalently, flipping the direction of the coordinate axes. You can convince yourself that this is the same as turning every object into its mirror image by holding your hands out in front of you, pointing your thumbs up, your index fingers towards each other, and your middle fingers towards yourself so that each hand has three fingers perpendicular to each other. If you rotate your left hand so that your thumb faces down, each corresponding finger between your left and right hand will be pointing in opposite directions. So parity and mirror symmetry are the same thing (up to some rotation).


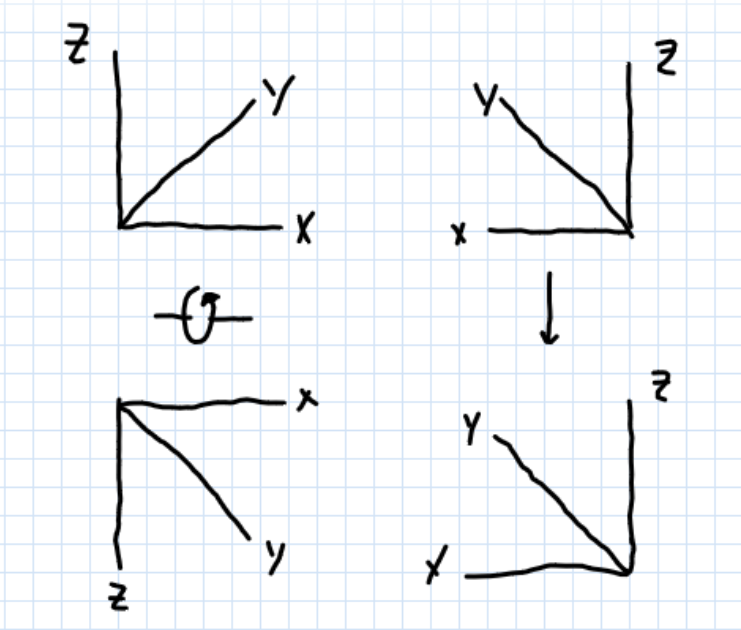A visualization of parity inversion expressed as a mirroring and a rotation

In classical mechanics, the parity properties of physical quantities can be tabulated by expressing them in terms of more basic quantities (such as $p=\dot{x}$, which flips sign under parity inversion, since $t$ stays the same but $x$ flips). There’s no major significance for parity in classical mechanics, though the formulation gives us our motivation for defining it in quantum mechanics.

In quantum mechanics, the parity operator $\hat{P}$ can be defined as the operator negating the matrix element for position with respect to some wavefunction basis:

\[\langle \psi_2 | \hat{x}| \psi_1 \rangle \mapsto -\langle \psi_2 |\hat{x}|\psi_1\rangle\]

This has two identical interpretations for how we achieve this using the $\hat{P}$ operator: we either map $\hat{x}$ to $P^\dagger \hat{x} P$, or map $|\psi_1\rangle$ to $P|\psi_1\rangle$, and obtain the $P^\dagger$ from the corresponding bra. This allows us to calculate the parity of operators acting on definite parity states. For example, the $\hat{L}$ operator has even parity, just like the parity of the $L=r \times p$ quantity from classical mechanics.

In quantum mechanics, parity symmetry appears in any situation where the Hamiltonian is parity-invariant. Since the kinetic term in the Hamiltonian is always an even function of position, it follows this condition is equivalent to the $V$ term also being an even function of position. Think about what types of systems automatically gain parity conservation from this alone!

Charge

Another example of a useful discrete transformation in the quantum world is that of charge conjugation. In the classical setting, this corresponds to negating the electric charge distribution of any physical bodies. On a larger scale, this has the effect of negating charges, currents, electric fields, and magnetic fields. As a result, Maxwell’s equations

\[\nabla \cdot \mathbf{E} = \frac{\rho}{\epsilon_0}\] \[\nabla \cdot \mathbf{B} = 0\] \[\nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t}\] \[\nabla \times \mathbf{B} = \mu_0(\mathbf{J} + \epsilon_0 \frac{\partial \mathbf{E}}{\partial t})\]

can be seen to be invariant under charge conjugation. In other words, classical electrodynamics is fundamentally charge-symmetric. In quantum mechanics, charge is usually a fixed parameter of the system, and there’s not much we can say about it at this point, but C-symmetry will play an important part when QFT comes into play.

Time

Time-reversal symmetry corresponds to playing videos of physical phenomena in reverse. Clocks tick backwards, and gravity carries balls uphill. One of the most important ways to describe this is by realizing that odd time derivatives become negated, while even derivatives do not. This way, both Newton’s second law

\[ F = m\ddot{x} \]

and Maxwell’s equations, given earlier, are invariant under time reversal. However, the quantum mechanical picture becomes complicated — it’s insufficient to perform our earlier trick of using the correspondence principle to perform the transformation $t \mapsto -t$. We must additionally perform the change $i \mapsto -i$. Under the assumption that the Hamiltonian is time-independent, the Schrodinger equation becomes time-reversal invariant². Beyond the complication of needing the complex conjugation transformation, the result is otherwise identical to the classical picture: T-symmetry is built into quantum mechanics.

QFT and Beyond

The Standard Model of particle physics is built upon Quantum Field Theory, a relativistic extension of quantum mechanics that considers the fundamental physical entities of nature to be quantum fields, with particles corresponding to excitations of these fields. The three fundamental forces of nature described by the Standard Model — the strong, weak, and electromagnetic forces — are each described by their own individual quantum field theories. During the early development of the SM, each force was thought to be C-, P-, and T-symmetric. However, in 1956 the Wu experiment detected parity-violation in Cobalt-60 beta decays, meaning the weak interaction was parity-asymmetric ³. Afterwards, the combined CP-symmetry was proposed to maintain some semblance of universal mirror-symmetry. However, in 1964 the Cronin-Fitch experiment discovered CP-violation in the decays of particles known as neutral kaons⁴.

What Now?

The discovery of CP-violation in the 1960s was devastating to the physics community, not only because it demonstrated a universal preference for chirality, but because of the numerous problems it suggested — problems that today remain unsolved. Some of these open questions include

Why does CP violation not occur in the strong force, even though the QCD Lagrangian permits it?
How does CP violation give rise to the observed matter-antimatter imbalance in the universe?

These major questions have led to the undertaking of numerous experiments studying decays of the B meson in hopes of understanding more:

BaBar, SLAC National Accelerator Lab, California
Belle/Belle II, KEKB/SuperKEKB, Japan
LHCb, CERN, France/Switzerland


The logo for the LHCb experiment at CERN.

In the coming years, these experiments are expected to observe new forms of CP violation, hopefully leading to new physics supporting theories beyond the Standard Model. (In fact, LHCb recently announced results about the possibility of lepton flavor universality violation⁵, a signifcant but unrelated development).

Noether, E. (1918). “Invariante Variationsprobleme”. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen. Mathematisch-Physikalische Klasse. 1918: 235-257. ↩
Sozzi, M.S. (2008). Discrete symmetries and CP violation. Oxford University Press. ISBN 978-0-19-929666-8. ↩
Wu, C. S.; Ambler, E.; Hayward, R. W.; Hoppes, D. D.; Hudson, R. P. (1957). “Experimental Test of Parity Conservation in Beta Decay”. Physical Review. 105 (4): 1413-1415. ↩
Christenson, J. H.; Cronin, J. W.; Fitch, V. L.; Turlay, R. (1964). “Evidence for the 2π Decay of the $K_0^2$ Meson System”. Physical Review Letters. 13 (4): 138. ↩
CERN (2021). “Intriguing new result from the LHCb experiment at CERN”. https://home.cern/news/news/physics/intriguing-new-result-lhcb-experiment-cern ↩